If I was trying to explain the concept of a probability distribution to a young child, this is the kind of animation I would use. I couldn't find a standard one, so I created my own.

While Darwin's picture of biological evolution was incredibly important in the history of scientific thought, some systems seem to elude it's elegant explanations. Here's a picture of the evolution of disease virulence (defined in terms of transmission rate and infection duration) for a variation of Bailey's lattice model. The curves represent the average population phenotype, and the color changes from black to yellow as time progresses. Some authors have observed that evolution seems to minimize infection duration while maximizing transmission rate. With a slight increase in mutation rate, though, we also can recover the Darwinian expectation of maximizing both transmission and duration. So, intuition still holds, but spatial population structure can introduce non-obvious complications into disease evolution.
The code for these simulations is available on GitHub or from me directly.

The sinusoidally forced pendulum can be described by a system of 3 autonomous ordinary differential equations \begin{align*} \frac{d x}{dt} &= 1 \\ \frac{d y}{dt} &= z \\ \frac{d z}{dt} &= \alpha \sin(\omega x) - \gamma \sin y \end{align*} This system exhibits chaotic dynamics. In fact, every possible binary sequence is encoded by the winding-number of the solution of this system for some initial condition on angle and velocity. The diagram shown here is one possible encoding that helps me visualize this sensitivity to initial condition.

In genetics theories of gene diversity and ecology theories of species diversity under neutral drift, one of the key results is to characterize the equilibrium distributions of frequencies. In Hubbell's neutral biodiversity theory, this was characterized by the equilibrium distribution of species under fixed immigration pressure.
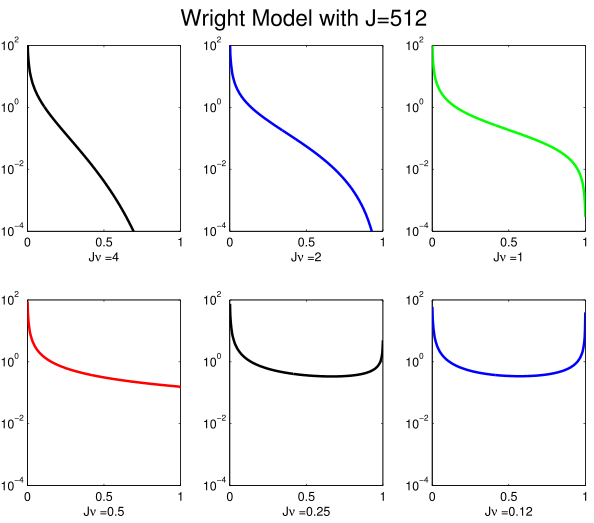
Another way to look at things, is to ask how many times in it's natural lifetime do we expect to observe a random species to have a particular abundance? This depends on the speciation rate \(\nu\) and the population size \(J\). It can be calculated very easily (up to a constant of proportionality) using the formula \[ \sum_{t=0}^{\infty} A^t p(0) = ( I-A)^{-1} p(0) \] where \(A\) is a \(J \times J\) matrix with \[ A_{yx} = \begin{cases} \frac{(1-\nu)x(J-x)}{J(J-1)} & \text{if} & x+1 = y \\ 1 - \frac{(1-\nu)x(J-x)}{J(J-1)} - \frac{x((J-x)+\nu (x-1)}{J(J-1)} & \text{if} & x = y \\ \frac{x((J-x)+\nu (x-1))}{J(J-1)} & \text{if} & x -1 = y \\ 0 & \text{otherwise} \end{cases} \] is the Markov generating matrix for a Wright--Fisher model and p(0) is a vector representing the initial population size distribution (all mass at 1). The figure at right shows that this distribution fundamentally changes behaviors when \( \nu J = 1/2 \)

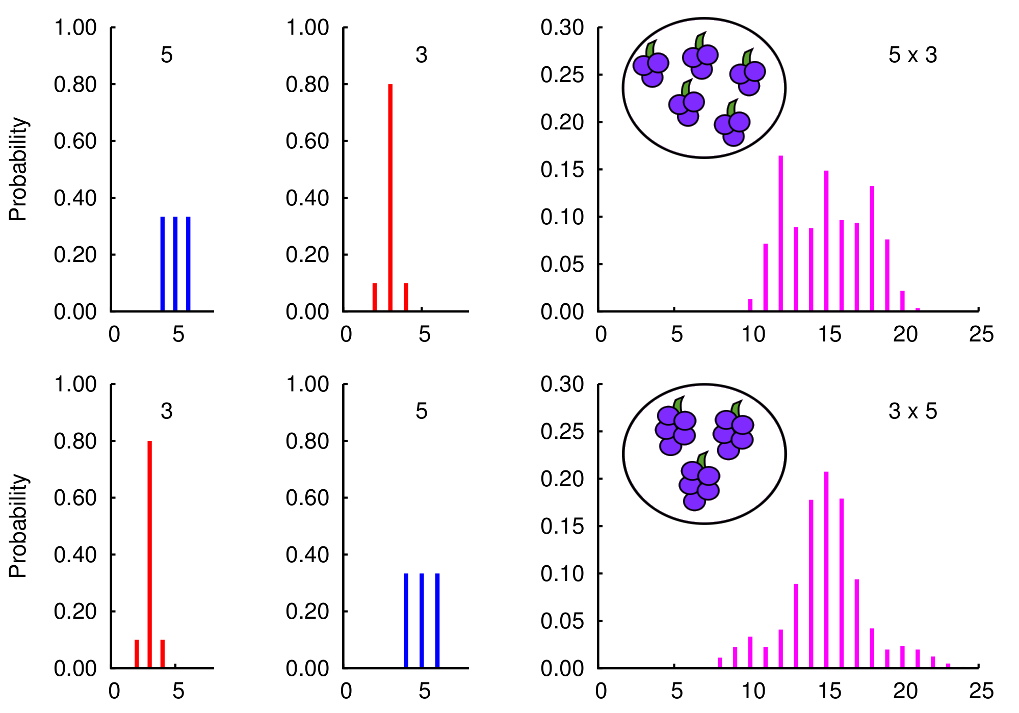
When we define multiplication, we usually ignore any aspects of uncertainty in the values we are multiplying. While the order of multiplication does not affect the expected value of an uncertain product, the order can change how the uncertainty is distributed around those expectations. Here is an illustrative example of the probability distributions for the number of grapes when we have 5 bunches of 3 or 3 bunches of 5.
[Link to related paper] and [Preprint version].

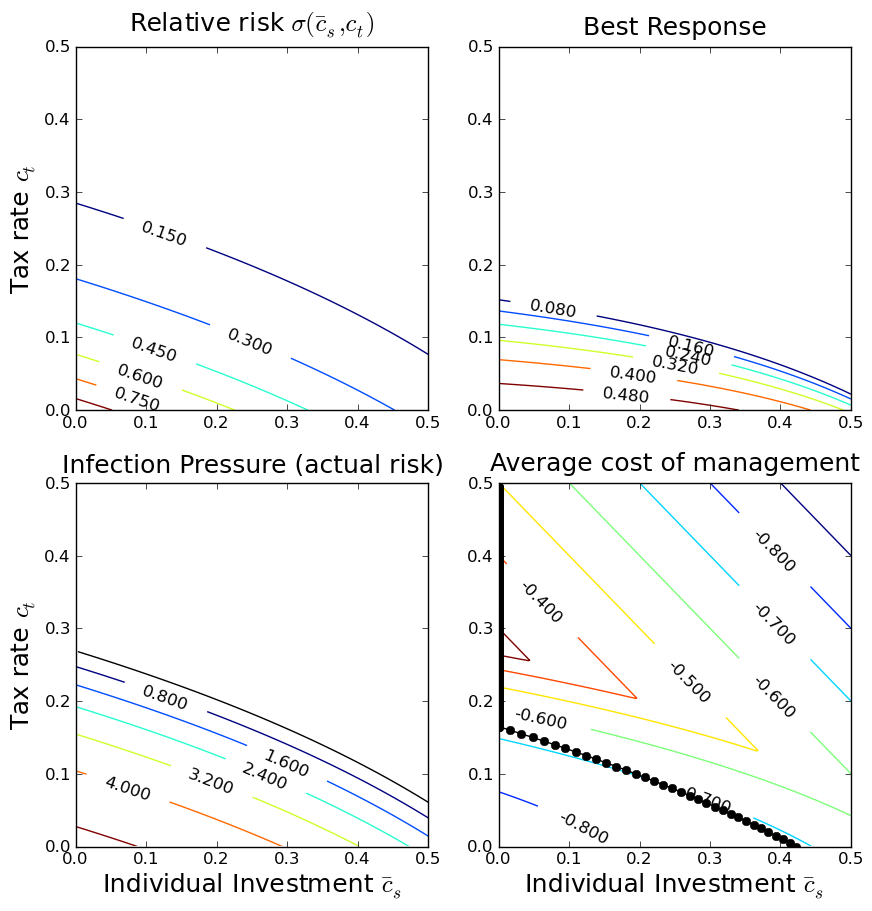
One very useful approach is public health policy design is that of the ``health commons'', where the economic motivations of individuals and the management inclinations of government feed back upon each other. This figure shows various components of a health-commons based policy analysis. We start out with a function that describes the effects of individual and government actions on exposures. Combined with a description of the disease biology, this determines the infection pressure and the actual risk of infection. Extending this analysis to include a game-theoretic analysis of individual responses, we can determine how the game equilibrium varies depending on the government taxation policy, and then determine the policy that has the best management outcomes.

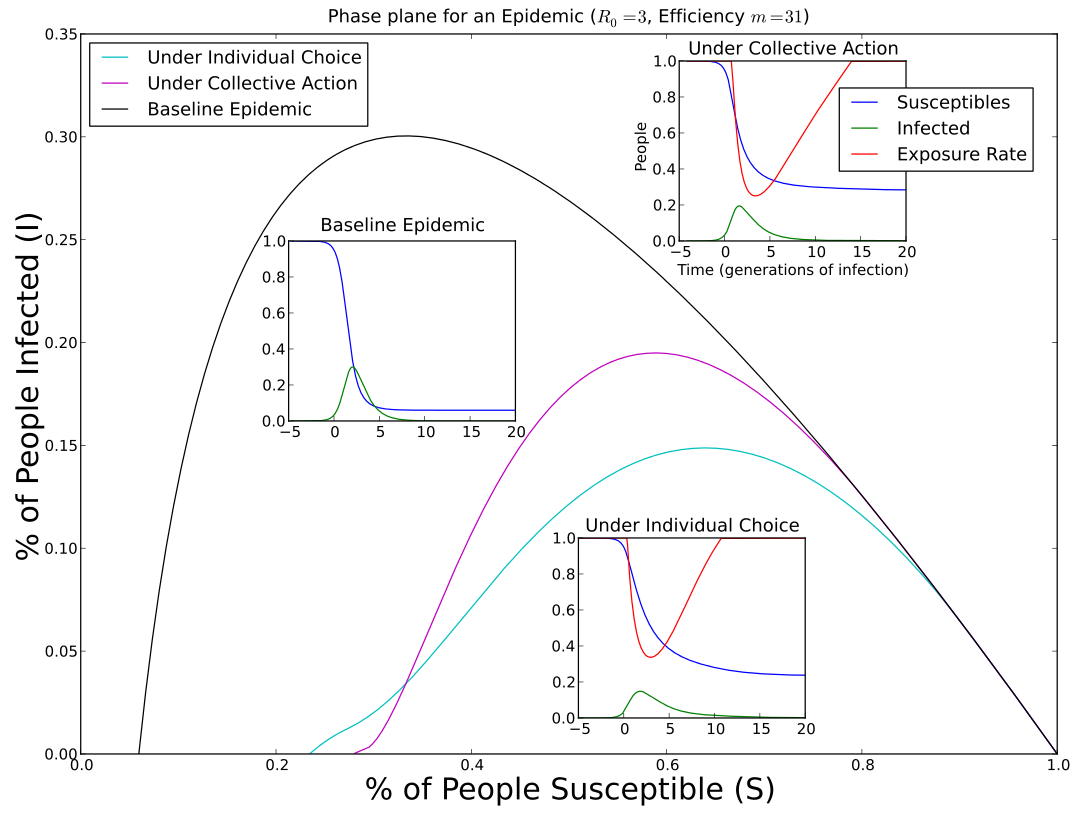
Social distancing is a universal method for coping with an epidemic. But the amount of social distancing that should be used depends on perspective. The optimal amount of social distancing for a community differs from the game equilibrium pattern of social distancing for individuals in that community. Optimal social distancing starts later, leading to a higher epidemic peak, but also ends later, leading to fewer total infections. This plot shows the phase-plane orbit for each, with their time series inset.
[Link to related paper]

In epidemic games with two interacting subpopulations, the equilibria structures are similar to those of Lotka competition models and Cournot duopoly models -- there may be no investments, the burden of investment may be carried by one group, or shared by both groups.
[Link to related paper]

One of the big questions in infectious disease dynamics is what interactions among individuals are important for disease transmission, and how do changes in those contacts change the rate of disease spread. Two classical descriptions of spatial interactions are the Distributed Contacts and Distributed Infectives hypotheses. The Distributed Contacts model says the important thing is our average contact distribution. The Distributed Infectives model says the important things are our short-term random contacts. This figure illustrates a unified theory where either hypothesis may can predict the speed of spatial spread, depending on how long it takes to relax to your average contact distribution.
[Link to related paper]

A model of hepatocyte homeostasis is combined with a drug-treatment model to match data for treatment of a patient with hepatitis C virus (HCV).
[Link to related paper]

For some infectious diseases, the morbidity of the disease changes depending on the age when a person gets sick -- some diseases are worse when you're old, and some are worse when you're young. This can make a big difference in how we handle the specific disease. For diseases that are worse when we are young, the balanced behavior is to always try to minimize transmission. But for diseases that are worse when we are old, either minimizing or maximizing transmission can be good practice for individuals in a community, depending on how much transmission can be controlled. This is sometimes referred to as endemic stability in vetrinary medicine. The plot shows strategy-invasion diagrams for these scenarios.
[Link to related paper]

Reaction networks based on mass-action kinetics can be represented as bipartite graph, with one type of node symbolizing each reaction, one type of node symbolizing the reactants, and directed edges representing the inputs and outputs of each reaction. These are also called hypergraphs, petri nets, and matroids. If the edges and nodes are labelled appropriately, the bipartite graph precisely represents a system of ordinary differential equations describing the dynamics of each reactant. This is better than simple graph-representations, which only represent linear effects correctly. Many simple mathematical descriptions of disease transmission can be formulated as reaction networks, so they can also be represented with bipartite graphs. For instance, this diagram represents disease-transmission in a species with two distinct stages in its life-history.
[Link to related paper]

A symmetric bifurcation diagram for a population model with error-prone culling. I find the comparison of this to the diagram for the classic logistic map interesting.

When points are Poisson-distributed in a plane, the distance at any location to the nearest point defines a random surface depending on the point locations and parameterized by the Poisson intensity. All the valleys of the surface are the same, but the peaks have random heights.

The simplest Archimedean spiral is constructed by successive bisection of radii and angles. The area of the spiral is a third the area of the inscribing circle. This figure was constructed with one of the first versions of the Geometer's Sketchpad, a piece of software released for Macintosh computers circa 1997. I believe the initial version was supported by an NSF grant.

Aaahhh! A buddy of mine who happens to be a member of a charismatic species sharing the planet with us.