
Archimedes and the sphere
When preparing some homework answers recently, I rediscovered a simple geometric fact that had escaped my attention in the past. If you have a ball, and place this ball in side the smallest can that is large enough to hold it and be sealed, the outside of the can, minus the top and bottom lids, has the exact same area as the ball inside! This is easy to check with the well-known formulas for the areas of spheres and cylinders. Not just that. If you slice the can into two parts with a level cut, in both cases, the area of the outside of that part of the can (minus the lid) will equal the outside area of the part of the ball left inside! This is a really rather remarkable coincidence (of course, I mean coincidence in the sense of coinciding, not in the sense of "lucky", because it's math after all). One of the reasons it may have escaped me is that this is a purely mathematical result that can not be applied in reality because solid materials are not fluidly deformable -- with a little experimentation, we learn that if you want to completely cover an orange in tinfoil, the tinfoil MUST BE longer than the height of the sphere, but you'll always have wrinkles when you do so.
This equality of areas reminded me of a result of Archimedes, which I'd heard the story of, but had never found so impressive. On looking it up, it seems that On the sphere and the cylinder does indeed include the first half of this result, atleast in its classical form.
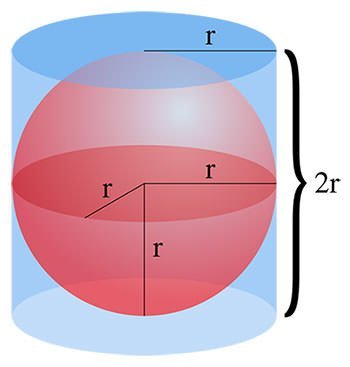
However, now I'm curious if his results imply the second of these considerations as well -- Did Archimedes also know about the equality of areas of the sliced cylinder and sphere sections? That would have been quite a splendid discovery, and worthy of a grave stone.